城市公交站点及换乘方案设计
设计要求
城市公共交通站点,站点之间的道路,及道路长度实际构成数学意义上的无向加权图。现请设计实现一个算法,求任意两站点间最短路径距离且输出该最短路径上的每个站点,然后给一个乘车换乘方案。
站点要求

数据结构设计
使用五个数组存放每条路线途径的站点
int L1[] = {1,2,3,4,6,9,8,11,14}; // 公交1路:9个站
int L2[] = {2,5,7,8,9,13,17}; // 公交2路:7个站
int L3[] = {10,9,12,15,19,22}; // 公交3路:6个站
int L4[] = {18,19,23,24,25}; // 公交4路:5个站
int L5[] = {13,16,20,21,25}; // 公交5路:5个站设计两个二维数组,用于后面的Floyd算法。
P存放各个站点之间的最短路径,D存放各个站点之间的最短路径的权值
//P[][]存放各个站点之间的最短路径,D[][]存放各个站点之间的最短路径的权值
int P[MAXVEX][MAXVEX],D[MAXVEX][MAXVEX];图的数据结构设计,顶点设计一个数组,用于存放此顶点途径的路线。
如果该顶点途径路线1和路线三,则再数组下标1和3上赋值1,3,不途径的赋值为零,如下图。
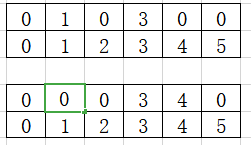
typedef struct
{
int name; //站点名称
int lines[6]; //途径路线
}Vertex;
typedef struct
{
Vertex vexs[MAXVEX]; //站点
int arc[MAXVEX][MAXVEX]; //邻接矩阵
int numVertexes, numEdges; //顶点数和边数
}MGraph;图的创建和初始化
创建图,把带权的邻接矩阵赋值进去,把每个顶点路径的路线也存放在顶点的lines数组中
/* 构造图 */
void CreateMGraph(MGraph *G)
{
int i, j;
//请输入边数和顶点数
G->numEdges=52;
G->numVertexes=26;
for (i = 0; i < G->numVertexes; i++)/* 初始化图的顶点编号 */
{
G->vexs[i].name=i;
}
for(i=0;i<26;i++)//初始化每个站点通过路线的数组,设为零
{
for(j=0;j<6;j++)
{
G->vexs[i].lines[j]=0;
}
}
G->vexs[1].lines[1]=1;
G->vexs[2].lines[1]=1; G->vexs[2].lines[2]=2;
G->vexs[3].lines[1]=1;
G->vexs[4].lines[1]=1;
G->vexs[5].lines[2]=2;
G->vexs[6].lines[1]=1;
G->vexs[7].lines[2]=2;
G->vexs[8].lines[1]=1; G->vexs[8].lines[2]=2;
G->vexs[9].lines[1]=1; G->vexs[9].lines[2]=2; G->vexs[9].lines[3]=3;
G->vexs[10].lines[3]=3;
G->vexs[11].lines[1]=1;
G->vexs[12].lines[3]=3;
G->vexs[13].lines[2]=2; G->vexs[13].lines[5]=5;
G->vexs[14].lines[1]=1;
G->vexs[15].lines[3]=3;
G->vexs[16].lines[5]=5;
G->vexs[17].lines[2]=2;
G->vexs[18].lines[4]=4;
G->vexs[19].lines[3]=3; G->vexs[19].lines[4]=4;
G->vexs[20].lines[5]=5;
G->vexs[21].lines[5]=5;
G->vexs[22].lines[3]=3;
G->vexs[23].lines[4]=4;
G->vexs[24].lines[4]=4;
G->vexs[25].lines[4]=4; G->vexs[25].lines[5]=5;
int t[MAXVEX][MAXVEX] = {0}; //构造无向带权图的邻接矩阵
t[1][2] = t[2][1] = 2;
t[2][3] = t[3][2] = 3;
t[2][5] = t[5][2] = 7;
t[3][4] = t[4][3] = 5;
t[4][6] = t[6][4] = 9;
t[5][7] = t[7][5] = 7;
t[6][9] = t[9][6] = 2;
t[7][8] = t[8][7] = 4;
t[8][9] = t[9][8] = 6;
t[8][11] = t[11][8] = 2;
t[9][10] = t[10][9] = 5;
t[9][12] = t[12][9] = 7;
t[11][14] = t[14][11] = 8;
t[12][15] = t[15][12] = 8;
t[13][9] = t[9][13] = 2;
t[13][16] = t[16][13] = 3;
t[13][17] = t[17][13] = 3;
t[15][19] = t[19][15] = 6;
t[16][20] = t[20][16] = 7;
t[18][19] = t[19][18] = 1;
t[19][22] = t[22][19] = 4;
t[19][23] = t[23][19] = 5;
t[20][21] = t[21][20] = 1;
t[21][25] = t[25][21] = 3;
t[23][24] = t[24][23] = 1;
t[24][25] = t[25][24] =
for (i = 0; i < G->numVertexes; i++)//* 初始化图
{
for ( j = 0; j < G->numVertexes; j++)
{
if (i==j)
G->arc[i][j]=0;
else
G->arc[i][j] = G->arc[j][i] = INFINITY;
}
}
for (i = 0; i < G->numVertexes; i++)//* 复制邻接矩阵
{
for ( j = 0; j < G->numVertexes; j++)
{
if(t[i][j] != 0)
{
G->arc[i][j] = t[i][j];
}
}
}
}Floyd算法求多源最短路径
Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,算法讲多源最短路径存放再P数组,最短路径的权值存放在D数组
/ Floyd算法,求网图G中各顶点v到其余顶点w的最短路径P[v][w]及带权长度D[v][w]。
void Floyd(MGraph G, int P[MAXVEX][MAXVEX],int D[MAXVEX][MAXVEX])
{
int v,w,k;
for(v=0; v<G.numVertexes; ++v) /* 初始化D与P */
{
for(w=0; w<G.numVertexes; ++w)
{
D[v][w]=G.arc[v][w]; /* D[v][w]值即为对应点间的权值 */
P[v][w]=w; /* 初始化P */
}
}
for(k=0; k<G.numVertexes; ++k)
{
for(v=0; v<G.numVertexes; ++v)
{
for(w=0; w<G.numVertexes; ++w)
{
if (D[v][w]>D[v][k]+D[k][w])/* 如果经过下标为k顶点路径比原两点间路径更短 */
{
D[v][w]=D[v][k]+D[k][w];/* 将当前两点间权值设为更小的一个 */
P[v][w]=P[v][k];/* 路径设置为经过下标为k的顶点 */
}
}
}
}
}
规划最短路径中的换乘方案,并输出
把两站的最短路径途径站站点,以及需要乘坐的公交路线规划出来,并输出。
void Transfer(MGraph *G,int L[MAXVEX])
{
int i=0,j=0,k=0;
for(i=0;i<25;i++)
{
for(j=1;j<6;j++)
{
if(G->vexs[L[i]].lines[j] == G->vexs[L[i+1]].lines[j])
{
if(G->vexs[L[i]].lines[j] != 0)
{
cout<<" 站点"<<L[k]<<" --(公交"<<G->vexs[L[i]].lines[j]<<"路)->";
k++;
break;
}
}
}
}
cout<<" 站点"<<L[k];
cout<<endl<<endl;
}输出最短路径
从P数组中输出两点的最短路径和距离,以及途径的站点的情况和数量。
void Dispath(MGraph *G,int P[MAXVEX][MAXVEX],int D[MAXVEX][MAXVEX])
{
int v,w,k;
int i=0;
int L[MAXVEX] = {0}; //存放两站之间的最短路径
cout<<" 输入出发站:站点";
cin>>v;
cout<<" 输入终点站:站点";
cin>>w;
cout<<endl<<" 站点"<<v<<" --> 站点"<<w<<" 距离:"<<D[v][w]<<"千米";
k=P[v][w]; /* 获得第一个路径顶点下标 */
cout<<" 路线: "<<v; /* 打印源点 */
L[i] = v;
while(k!=w) /* 如果路径顶点下标不是终点 */
{
cout<<" -> "<<k; /* 打印路径顶点 */
i++;
L[i] = k;
k=P[k][w]; /* 获得下一个路径顶点下标 */
}
L[i+1]=w;
cout<<" -> "<<w<<" 共 "<<i+1<<" 站"<<endl<<endl;
Transfer(G,L);
}主函数
创建图,调用Floyd算法最短路径,输出最短路径和换乘的路线
int main()
{
MGraph G;
CreateMGraph(&G);
Floyd(G,P,D);
Dispath(&G,P,D);
}输出结果
总结
1.数据结构设计不够完美,路线的数据结构用链表可能会更好
2.功能不够丰富,没有规划最少换乘的路线,途径站点最少的路线

